Teoría de Categorías

Christian Chávez
Universidad Yachay Tech
2023
Un poco de historia
Samuel Eilenberg (izquierda) y Saunders Mac Lane introducieron la teoría de la categoría a mediados del siglo XX, como parte de su trabajo en topología algebraica.


¿De qué se trata la Teoría de Categorías?
Empecemos por lo que no es
- No es una teoría para categorizar objetos matemáticos
- No se limita al estudio de un solo tipo de estructura matemática
- No es una teoría del todo
A breves rasgos, la teoría de categorías es...
- una teoría matemática sobre estructura
- un lenguaje para estudiar diferentes áreas de las matemáticas
- "la matemática de las matemáticas" (Eugenia Cheng)
Motivación
Diferentes áreas tienen similitudes fundamentales
Teoría de Grupos
Topología

Álgebra Lineal

Antes que nada, necesitamos algunos conceptos preliminares
1
Los conjuntos no son suficientes
- No toda colección de objetos que se puede describir con una propiedad es un conjunto
- El problema es que tales descripciones pueden dar lugar a colecciones "muy grandes" para ser consideradas conjuntos
1
Los conjuntos no son suficientes
Definición. Una clase es una colección de objetos matemáticos, que se puede describir mediante una propiedad.
- Todo conjunto es una clase, pero no al revés
- Todo conjunto es elemento de algún otro conjunto, pero...
- hay clases que no son elementos de ninguna otra clase
2
Terminología, notación y más terminología
- Morfismo, mapa (mapping): una función, grosso modo
- $\longrightarrow$ representa un morfismo
- Objeto: cualquier cosa definida formalmente
- $\bigcirc$ representa un objeto
- Diagrama: representación visual de relaciones entre objetos por medio de flechas
2
Terminología, notación y más terminología
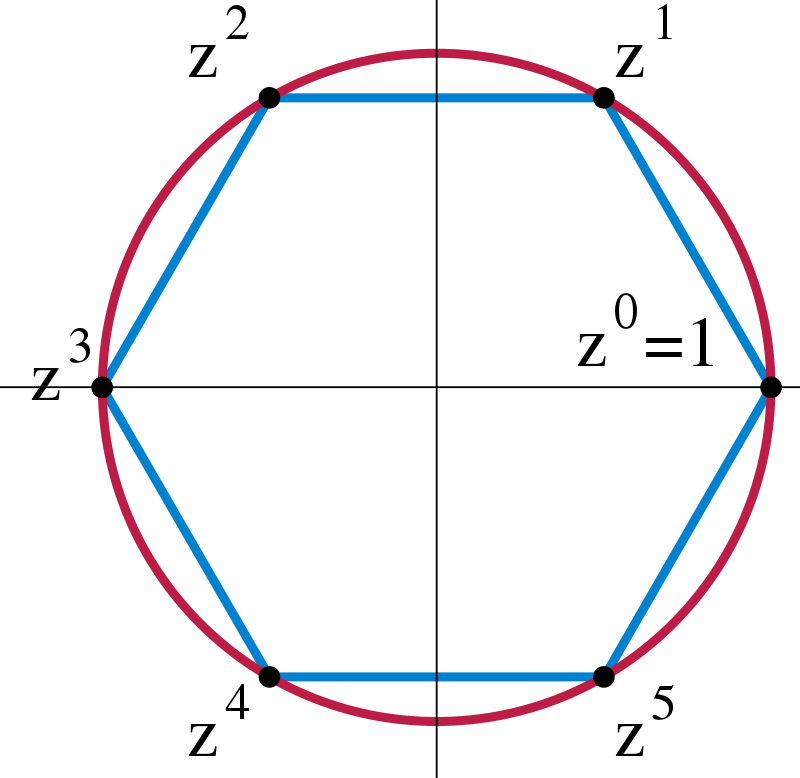
- Un morfismo entre objetos $A$ y $B$: se denota $$ f : A \to B\qquad\text{o} \qquad A \xrightarrow{f} B $$
Ejemplo: un diagrama (conmutativo)
En la teoría de categorías, los diagramas conmutativos son análogos a las ecuaciones en álgebra.
Categorías
Categorías
Definición. Una categoría $\mathscr{C}$ consiste de $4$ partes y $2$ reglas:
- Una clase de objetos $\mathbf{ob}(\mathscr{C})$
- Una clase de morfismos $\mathbf{hom}(A, B)$ por cada par de objetos $A, B \in \mathbf{ob}(\mathscr{C})$
- Composición: por cada $A, B, C\in \mathbf{ob}(\mathscr{C})$, existe un morfismo $$ \begin{array}{ccc} \mathbf{hom}(B, C) \times \mathbf{hom}(A, B) &\to& \mathbf{hom}(A, C) \\ (g, f) &\mapsto& g \circ f \end{array} $$
- Una identidad $1_A \in \mathbf{hom}(A, A)$ por cada $A\in \mathbf{ob}(\mathscr{C})$
Categorías
Definición. Una categoría $\mathscr{C}$ consiste de $4$ partes y $2$ reglas:
- Asociatividad: para todo $f\in \mathbf{hom}(A, B)$, $g\in \mathbf{hom}(B, C)$, y $h\in \mathbf{hom}(C, D)$ se cumple $$ (h\circ g) \circ f = h\circ (g\circ f) $$
- Para todo $f\in \mathbf{hom}(A, B)$, se tiene $$ f\circ 1_A = f = 1_B \circ f $$
Categorías (en resumen)
- Objetos
- Morfismos
- Composición
- Identidades
- La composición es asociativa
- Propiedad de identidad
Ejemplos de Categorías
Ejemplos de Categorías
$\mathbf{Set}$
Ejemplos de Categorías
$\mathbf{Set}$
La categoría de todos los conjuntos
- Objetos: conjuntos
- Morfismos: funciones entre conjuntos
- Composición: usual, $(f \circ g) (x) = f(g(x))$
- Identidades: $1_A(x) = x, \forall x\in A$, por cada conjunto $A$
$\mathbf{Set}$
- $\circ$ es asociativa: para todo $f\in \mathbf{hom}(A, B)$, $g\in \mathbf{hom}(B, C)$, y $h\in\mathbf{hom}(C, D)$, tenemos $$ \begin{align*} ((f\circ g) \circ h) (x) &= (f\circ g)(h(x))\\ &= f(g(h(x)))\\ &= f((g\circ h)(x))\\ &= (f\circ (g\circ h))(x) \end{align*} $$
$\mathbf{Set}$
Ejemplos de Categorías
$\mathbf{Grp}$
La categoría de todos los grupos $(G, \cdot)$
- Objetos: grupos
- Morfismos: homomorfismos de grupos
- Composición: usual, $(f \circ g) (x) = f(g(x))$
- Identidades: $1_A(x) = x$, por cada conjunto $A$
Ejemplos de Categorías
$\mathbf{Top}$
La categoría de todos los espacios topologicos $(X, \mathcal{T})$
- Objetos: espacios topologicos
- Morfismos: funciones continuas
- Composición: usual, $(f \circ g) (x) = f(g(x))$
- Identidades: $1_A(x) = x$, por cada conjunto $A$
Ejemplos de Categorías
$(\mathbb{R}, \leq)$
Una categoría "del orden"
- Objetos: números reales
- Morfismos: un único $\varphi : x\to y$ t.q. $x\leq y$
- Composición: $x\rightarrow{} y \rightarrow{} z$ da lugar $x\rightarrow{} z$ t.q. $x\leq z$
- Identidades: $1_x = x$ para todo $x\in \mathbb{R}$. Claramente $x\leq x$
- Las reglas de composición e identidades son inmediatas
Morfismos especiales
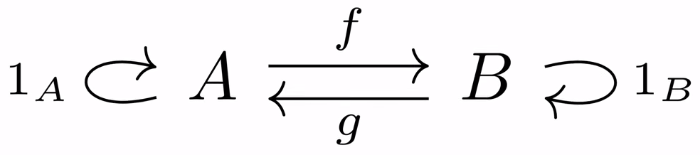
En una categoría $\mathscr{A}$, llamamos isomorfismo a cualquier morfismo $f: A\to B$, con $A,B\in \mathscr{A}$, tal que existe $g: B \to A$ y este diagrama conmuta, i.e.,
- $1_A = g \circ f$, y
- $ 1_B = f\circ g $.
Escribimos $g= f^{-1}$
Functores
Functor
- En teoría de categorías, siempre nos preguntamos por los mappings entre pares de objetos
- Incluso si esos objetos son categorías
- Un mapeo entre categorías se denomina functor
Functor
Definición. Sean $\mathscr{A}$ y $\mathscr{B}$ categorías. Un functor $F : \mathscr{A} \to \mathscr{B}$ consiste de dos objetos que satisfacen dos condiciones:
- una función de objetos $\mathbf{ob}(\mathscr{A}) \to \mathbf{ob}(\mathscr{B})$, tal que $X\mapsto F(X)$
- una función de morfismos $\mathbf{hom}(X, Y) \to \mathbf{hom}(F(X), F(Y))$
- Se respeta la composición: $$F(f\circ g) = F(f)\circ F(g)$$ siempre que $X\xrightarrow{g} Y\xrightarrow{f} Z$ en $\mathscr{A}$
- Se preservan las identidades: $F(1_A) = 1_{F(A)},\forall A\in \mathscr{A}$
Ejemplos de Functores
$\mathcal{I}: \mathscr{C} \to \mathscr{C}$
El functor identidad
- Envía cada objeto y cada morfismo a sí mismo
Ejemplos de Functores
$U: \mathbf{Grp} \to \mathbf{Set}$
El functor que remueve la estructura
- Si $G$ es un grupo, $U(G)$ es el conjunto del grupo, i.e., $ (G, \cdot) \mapsto G $
- Si $\varphi : G \to H$ es un homomorfismo de grupos, $U(\varphi)$ es la función $\varphi$, i.e., $$ (G,\cdot) \xrightarrow{\varphi} (H, *) \quad\mapsto\quad G\xrightarrow{\varphi} H $$
Transformaciones Naturales
Mapas entre functores

Transformaciones Naturales
En un principio, la motivación para introducir categorías y functores fue formalizar esta idea
Transformaciones Naturales
La noción de morfismos entre functores solo tiene sentido cuando los functores tienen el mismo dominio y codominio.
$$ \mathscr{A} \xrightarrow{F,\,G} \mathscr{B} $$
Queremos "transformar" un functor en otro pero manteniendo la estructura interna (del dominio y codominio).
Transformaciones Naturales
Definición. Sean $\mathscr{A}, \mathscr{B}$ categorías y $F, G$ functores de $\mathscr{A}$ a $\mathscr{B}$. Una transformación natural $\alpha$ de $\mathscr{A}$ a $\mathscr{B}$ es una familia de morfismos $$\left( F(A)\xrightarrow{\alpha_A} G(A)\right)_{A\in \mathscr{A}}$$ en $\mathscr{B}$ tal que si $f: A \to A'$ es un morfismo en $\mathscr{A}$, entonces el siguiente diagrama conmuta:
Transformaciones Naturales
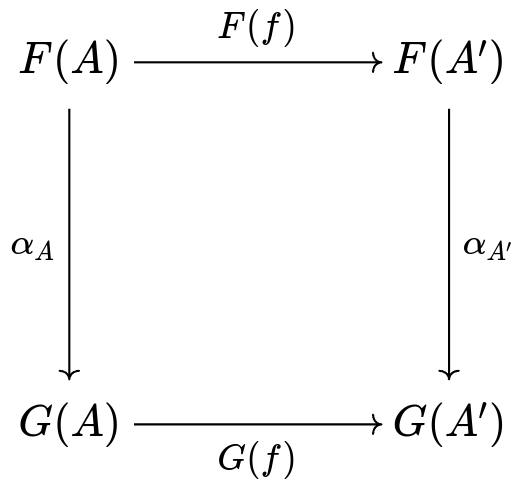
Transformaciones Naturales
Observaciones
- Esta definición se dió de tal manera que por cada $A\xrightarrow{f} A'$ en $\mathscr{A}$ se pueda contruir exactamente un morfismo $F(A) \to G(A')$ en $\mathscr{B}$.
- Dicho morfismo es la diagonal del diagrama anterior
Ejemplo
$\left( 1_{F(A)}\right)_{A\in \mathscr{C}}$
La identidad: una transformación natural de $F$ a sí mismo
- para cualquier par de categorías $\mathscr{C}$ y $\mathscr{D}$
- y cualquier functor $F$ de $\mathscr{C}$ a $\mathscr{D}$
Ejemplo
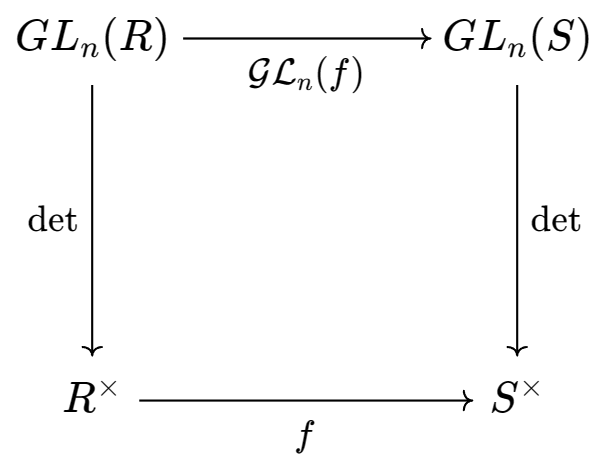
$\mathrm{\det}$
- Sea \(\mathcal{G} \mathcal{L}_n\) el funtor de $\mathrm{CRing}$ a $\mathrm{Grp}$ tal que cada \(R\in \mathrm{CRing}\) se mapea por \(\mathcal{G} \mathcal{L}_n\) al grupo \(GL_n(R)\) de matrices invertibles \(n \times n\) con entradas de \(R\).
- Para cada homomorfismo de anillos \(f: R \rightarrow S\), tenemos que \(\mathcal{G} \mathcal{L}_n(f)\) es el mapeo de matrices que aplica \(f\) a cada entrada de la matriz
- Dado que \(f\) envía el elemento neutro 1 a 1, se sigue que \(\mathcal{G} \mathcal{L}_n(f)\) envía matrices invertibles a matrices invertibles
Ejemplo
$\mathrm{\det}$
- Sea \(\mathcal{G}\) el funtor de $\mathrm{CRing}$ a $\mathrm{Grp}$ que mapea cada anillo \(R\) a su grupo de unidades \(R^{\times}\), y cada homomorfismo de anillos \(f\) a su restricción a los grupos de unidades (también denotado por \(f\)).
- La determinante es una transformación natural de \(\mathcal{G} \mathcal{L}_n\) a \(\mathcal{G}\) porque la determinante está definida por el mismo polinomio para todos los anillos, de modo que el siguiente diagrama es conmutativo:
Ejemplo
$\mathrm{\det}$
Aplicaciones de la Teoría de Categorías
Aplicaciones de la Teoría de Categorías
- Álgebra homológica
- Ciencias de la computación
- Programación fucional, e.g., Haskell
- Teoría de cARTEgorías