I found nowhere the explicit computation of the interleaving distance between interval modules, so I decided to post it here.

Preliminaries

Let $\mathbf{k}$ be an arbitrary field, fixed throughout. We denote by $\mathbb{R}$ either the real line or the category induced by the poset $(\mathbb{R},\leq)$. All functors are covariant.

The category of persistence modules

A persistence module is a functor $\mathbb{R}\to \mathrm{Vect}(\mathbf{k} )$.

Example 1. Let $I\subset \mathbb{R}$ be an interval. Define $\mathbf{k}^I\colon \mathbb{R}\to \mathrm{Vect}(\mathbf{k} )$ by

\[\begin{align*} t \;&\longmapsto\; \begin{cases} \mathbf{k} & \text{if } t \in I, \\ \mathbf{0} & \text{else} \end{cases}\\ (r \to s) \;&\longmapsto\; \begin{cases} \mathbf{k} \xrightarrow{\mathrm{Id}} \mathbf{k} & \text{if } r,s \in I, \\ \mathbf{0} & \text{else} \end{cases} \end{align*}\]

on objects and morphisms, respectively. Here $\mathbf{0}$ denotes both the zero vector space and the zero map, respectively. We call $\mathbf{k}^I$ the interval module over $I$. We usually denote $\mathbf{k}^I(t)$ by $\mathbf{k}^I_t$.

The concise definition of persistence module can be restated. Let $V\colon \mathbb{R}\to \mathrm{Vect}(\mathbf{k} )$ be a persistence module.

  • For each $t\in \mathbb{R}$ and each arrow $r\to s$, we denote $V(t)=V_t$ and $V(r\to s) = v_s^r$.

  • Since $V$ is a functor, we have the so-called composition law: $v_t^s\circ v_s^r = v_t^r$ whenever $ r\leq s\leq t$, and $ v_t^t = \mathrm{Id}_{V_t}$.

Therefore, a persistence module $V$ consists of a family $(V_t)_{t\in \mathbb{R}}$ of vector spaces together with a family

\[\left(v_t^s \colon V_s\to V_t\mid s\le t\right)_{s,t\in\mathbb{R}}\]

of linear maps.

This set-theoretical definition is equivalent to the categorical one above.

Since persistence modules are functors, we can consider the natural transformations between them, and since those can be composed (using vertical composition) we obtain a functor category.

Definition 1. The category of persistence modules is $\mathrm{Fun}(\mathbb{R}, \mathrm{Vect}(\mathbf{k} ))$.

More specifically, a morphism of persistence modules $\alpha\colon U\to V$ is a family of linear maps $(\alpha_r\colon U_r\to V_r)_{r\in \mathbb{R}}$ that make the diagram

\begin{tikzcd} U_s \arrow[r, "u_t^s"] \arrow[d, "\alpha_s"'] & U_t \arrow[d, "\alpha_t"] \\ V_s \arrow[r, "v_t^s"] & V_t \end{tikzcd}

commute for all $s\le t$, i.e. $v_t^s\circ \alpha_s=\alpha_t\circ u_t^s$.

Example 2. If $U$ and $V$ are any persistence modules, then there is a zero morphism $U\to V$, given by $( U_r\xrightarrow{\mathbf{0}} V_r)_{r\in\mathbb{R}}$, and denoted by $\mathbf{0}$.

Example 3 (A non example). Consider the interval modules $\mathbf{k}^{[0,1]}$ and $\mathbf{k}^{[0,2]}.$ For each $r\in \mathbb{R}$, define

\[\alpha_r = \mathbf{k}^{[0,1]}_r\to\mathbf{k}^{[0,2]}_r \quad\text{by}\quad x\mapsto x.\]

Note that $\alpha=(\alpha_r)_{r\in\mathbb{R}}$ is the inclusion $\mathbf{k}^{[0,1]}\hookrightarrow\mathbf{k}^{[0,2]}.$ However, $\alpha$ is not a morphism of persistence modules. For example, for the arrow $1\to 2$ we have

\[\begin{align*} \mathbf{k}^{[0,1]}(1 \to 2) &= \mathbf{k} \xrightarrow{\mathrm{0}} \mathbf{0}, \\[0.5em] \mathbf{k}^{[0,2]}(1 \to 2) &= \mathbf{k} \xrightarrow{\mathrm{Id}} \mathbf{k}, \\[0.75em] \alpha_1 &= \mathbf{k} \xrightarrow{\mathrm{Id}} \mathbf{k}, \\ \alpha_2 &= \mathbf{0} \xrightarrow{\mathrm{0}} \mathbf{k}. \end{align*}\]

Then the diagram \begin{tikzcd} \mathbf{k} \arrow[r, "0"] \arrow[d, "\mathrm{Id}"'] & \mathbf{0} \arrow[d, "0"] \\ \mathbf{k} \arrow[r, "\mathrm{Id}"'] & \mathbf{k} \end{tikzcd}

does not commute.

The shift functor

Let $U$ be a persistence module and fix any $t\in \mathbb{R}$. Define a new persistence module $U[t]$ by

\[U[t](r) = U_{r+t} \quad\text{and}\quad U[t](r\to s) = u_{s+t}^{r+t}.\]

We say that $U[t]$ is a shifted module. Note that

\[U[0]=U \quad\text{and}\quad U[t][t'] = U[t+t']\]

for any $t,t’\in \mathbb{R}$. Similarly, for any morphism of persistence modules $\alpha\colon U\to V$, we can define a shifted module morphism by $\alpha[t] = (\alpha_{r+t})_{r\in \mathbb{R}}$.

Suppose we’ve made two shifts of $U$, say $U[s]$ and $U[t]$, where $s\leq t$. We might ask what is the relationship between these shifted modules? In other words, we wonder if there is a canonical natural transformation $\alpha\colon U[s]\to U[t]$. To find out, consider any $p\to q$ and apply both $U[s]$ and $U[t]$ to this arrow. We get

\[U[s](p\to q)\; =\; U_{p+s}\xrightarrow{u_{q+s}^{p+s}} U_{q+s}\]

and

\[U[t](p\to q) \;=\; U_{p+t}\xrightarrow{u_{q+t}^{p+t}} U_{q+t}.\]

Since $\alpha=(\alpha_r )_{r\in \mathbb{R}}$ is determined by its components, we need to find the vertical arrows that make the square

\begin{tikzcd} U_{p+s} \arrow[r, "u_{q+s}^{p+s}"] \arrow[d, "\alpha_p"'] & U_{q+s} \arrow[d, "\alpha_q"] \\ U_{p+t} \arrow[r, "u_{q+t}^{p+t}"'] & U_{q+t} \end{tikzcd}

commute. By setting $\alpha_p = u_{p+t}^{p+s}$ and $\alpha_{q}=u_{q+t}^{q+s}$, the composition law give us

\[u_{q+t}^{p+t} \circ u_{p+t}^{p+s} = u_{q+t}^{p+s} = u_{q+t}^{q+s}\circ u_{q+s}^{p+s},\]

which means the square commutes. So, yes, there is a canonical way to map $U[s]$ to $U[t]$. We define

\[U[s]\xrightarrow{U[s\to t]} U[t]\;\; = \;\;\left( u_{r+t}^{r+s} \right)_{r\in \mathbb{R}}\]

and denote $\alpha = U[s\to t]$.

Remark.

  • For $t\geq 0$, we denote $\mathbb{1}^{t}_U = U[0\to t]$.

  • Observe that

    \[\mathbb{1}^{0}_U = U[0\to 0] = (u_r^r)_{r\in \mathbb{R}} = (\mathrm{Id}_{U_r})_{r\in \mathbb{R}} =\mathbb{1}_{U}\]

    is an identity natural transformation. So, for $t\geq 0$, we might think of $\mathbb{1}^{t}_U$ as a generalized identity.

  • By definition, we get $U[t\to t] = \mathbb{1}_{U[t]}$ for any $t\in \mathbb{R}$. Moreover, if $r\leq s\leq t$, for any $p\in \mathbb{R}$ we have

    \[\begin{aligned} \left( U[s\to t] \circ U[r\to s] \right)_p &= U[s\to t]_p \circ U[r\to s]_p\\ &= u_{p+t}^{p+s} \circ u_{p+s}^{p+r}\\ &= u_{p+t}^{p+r}\\ &= U[r\to t]_p \end{aligned}\]

    by the composition law. Thus

    \[U[s\to t] \, \circ\, U[r\to s] \, =\, U[r\to t].\]

The last remark leads us to the following definition.

Definition 2. Let $\mathbf{X} = \mathrm{Fun}(\mathbb{R}, \mathrm{Vect}(\mathbf{k} ))$ be the category of persistence modules. The shift functor $T\colon \mathbb{R}\to \mathrm{End}(\mathbf{X})$ is defined as follows:

  • Objects: for each $t\in \mathbb{R}$, we have a functor $T(t) \colon \mathbf{X}\to \mathbf{X}$ denoted $T_t$ and defined by

    \[T_t( U) = U[t],\quad T_t(\alpha) = \alpha[t]\]

    on objects $U\in \mathbf{X}$ and morphisms $\alpha=(\alpha_r)_{r\in \mathbb{R}}$, respectively.

  • Morphisms: for each $r\to s$, we have a natural transformation $T(r\to s)\colon T_r\to T_s$ defined by

    \[T(r\to s) = \left( U[r\to s] \right)_{U\in \mathbf{X}}.\]

We prefer the notation $[\,\cdot\,]$ rather than $T$.

Example 4 (Shifts of an interval module). Let $\mathcal{I}=\mathbf{k}^I$ be an interval module and fix $t\in \mathbb{R}$. Then, for each $r\in \mathbb{R}$ we have

\[\begin{align*} \mathbf{k}^I(r+t) &= \begin{cases} \mathbf{k} & \text{if } r+t \in I, \\ \mathbf{0} & \text{else} \end{cases} \\ &= \begin{cases} \mathbf{k} & \text{if } r \in I - t, \\ \mathbf{0} & \text{else} \end{cases} \\ &= \mathbf{k}^{I - t}(r) \end{align*}\]

and similarly, for each $r\leq s$ we have

\[\mathbf{k}^I(r+t\to s+t) = \mathbf{k}^{I-t}(r\to s).\]

Thus $\mathbf{k}^I[t] = \mathbf{k}^{I-t}$. We will denote $\mathcal{I}[t]=\mathcal{I}-t$.

The interleaving distance between persistence modules

Let $U$ and $V$ be persistence modules and $t$ a real number. A $t$-interleaving of $U$ and $V$ is a pair of natural transformations $(\phi\colon U\to V[t], \; \psi\colon V\to U[t] )$ that make the diagrams

tikzcd diagram

commute. If such a pair exists, we say that $U$ and $V$ are $t$-interleaved.

Example 5. Two persistence modules are isomorphic if and only if they are $0$-interleaved. Thus, we can think of interleavings as generalized isomorphisms.

Definition 3. The interleaving distance between two persistence modules $U$ and $V$ is

\[d_T (U, V)=\inf \left\{t\geq 0 \mid U \text { and } V \text{ are }t\text{-interleaved}\right\}.\]

in case there is at least one interleaving of $U$ and $V$. If no such interleaving exists, we set $d_T (U, V)= \infty$.

The subscript $T$ remind us that $d_T$ depends on the shift functor. We must keep in mind that $d_T$ is not an actual metric but a pseudometric, because we could have $d_T (U, V)=0$ even if $U\neq V$.

The computation

We’ll do the computation of $d_T(\mathbf{k}^I,\mathbf{k}^J)$ for the case of closed intervals. Let $I=[a,b]$ and $J=[c,d]$. Denote by $\mathcal{I}=\mathbf{k}^I$ and $\mathcal{J}=\mathbf{k}^J$ the associated interval modules.

Our strategy is to find some appropriate bounds for $d_T (\mathbf{k}^I,\mathbf{k}^J)$. Before going into the search for the pair of morphisms that would make the triangles above commute, we need to understand the morphisms between arbitrary interval modules, because then we can characterize the morphisms between shifted interval modules.

Let $\alpha\colon \mathbf{k}^I\to \mathbf{k}^J$ be any persistence module morphism. For each $t\in \mathbb{R}$ we have a map of vector spaces $\alpha_t \colon \mathbf{k}^I_t\to \mathbf{k}^J_t$ and we know that the only possible options for $\mathbf{k}^I_t$ and $\mathbf{k}^J_t$ are either $\mathbf{k}$ or $\mathbf{0}$. The following figure illustrates the “behaviour” of an interval module respect to the position of the input arrow.

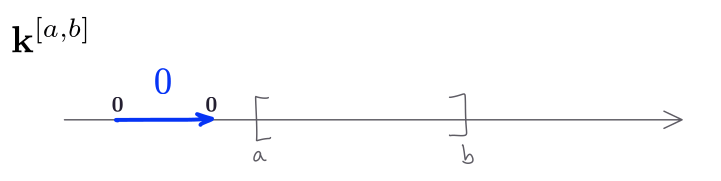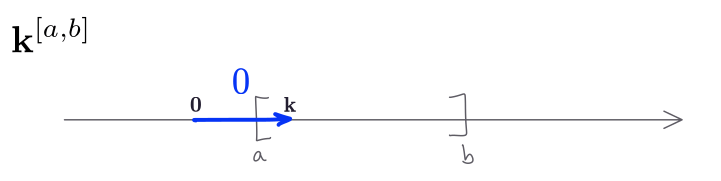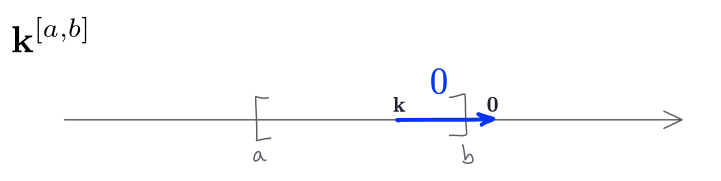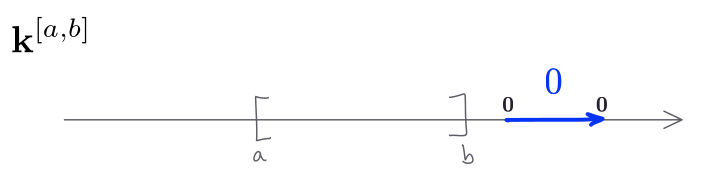
Interval module

Note that, if $t\notin I\cap J$, then either $\mathbf{k}^I_t=\mathbf{0}$ or \(\mathbf{k}^J_s=\mathbf{0}\), and in any case $\alpha_s$ is the zero map. Thus, we always get zero morphisms outside of the intersection. Inside the intersection we have a linear map $\alpha_t\colon \mathbf{k}\to \mathbf{k}$ for each $t\in I\cap J$, and since $\mathbf{k}$ is a field, $\alpha_t$ is nothing more than multiplication by some scalar $\lambda\in \mathbf{k}$, so $\alpha_t\colon x\mapsto \lambda x$. Such $\lambda$ could be zero, though.

As a first result, we have the following.

Fact 1. If $I\cap J=\varnothing$, then $\mathrm{Hom}(\mathbf{k}^I, \mathbf{k}^J) = \mathbf{0}$.

With this trivial case out of the way, assume $I\cap J\neq \varnothing$, and let us consider two cases: $a < c$ or $c\leq a$.

  1. Suppose $a < c$. Let us focus on $\alpha_t\colon \mathbf{k}^I_t \to \mathbf{k}^J_t$ with $t\in I\cap J$, i.e. with $c\leq t\leq b.$ The case when $t\notin I\cap J$ give us $\alpha_t=0$ as noted earlier and is illustrated by the following figure:

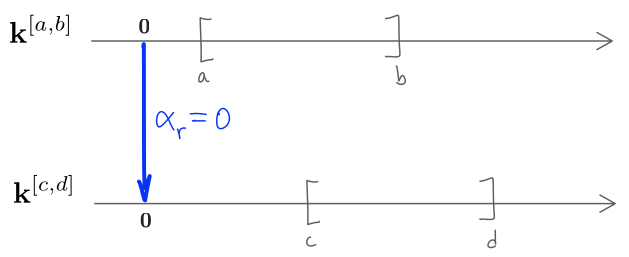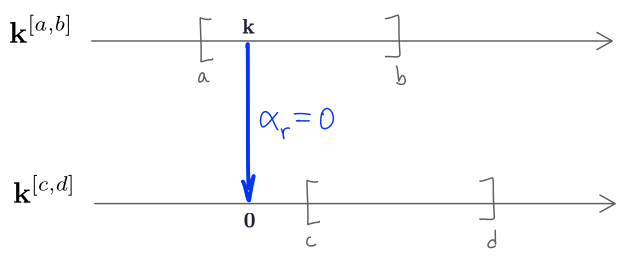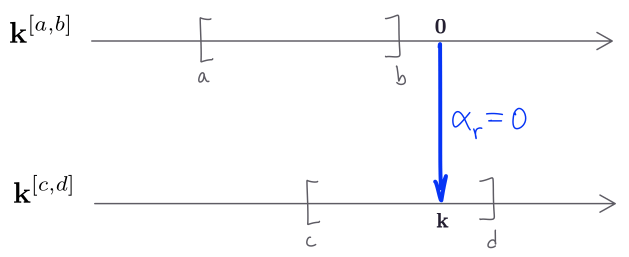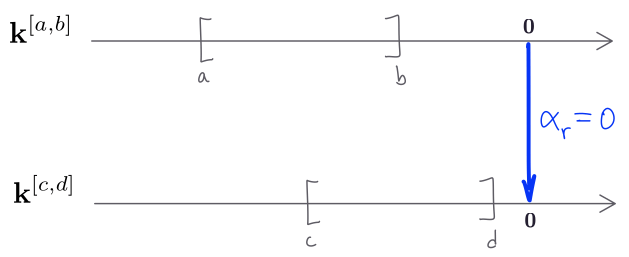
    Interval module

    Take the arrow $a\to t$ and apply both $\mathbf{k}^I$ and $\mathbf{k}^J$. We have $\mathbf{k}^I(a\to t) = \mathbf{k}\xrightarrow{\mathrm{Id}} \mathbf{k}$ and $\mathbf{k}^J(a\to t) = \mathbf{0}\xrightarrow{\mathrm{0}} \mathbf{k}$. Note that $\alpha_a\colon \mathbf{k}\to \mathbf{0}$ is the zero map and $\alpha_t\colon \mathbf{k}\to \mathbf{k}$ is some linear map. Naturality implies

    \[\alpha_t = \alpha_t\circ \mathbf{k}^I(a\to t) = \mathbf{k}^J(a\to t)\circ \alpha_a = 0.\]

    Thus $\alpha_t$ is zero even on $I\cap J$. The conclusion is that $\mathrm{Hom}(\mathbf{k}^I, \mathbf{k}^J)\cong \mathbf{0}$ because $I$ was born before $J$.

  2. Suppose $c\leq a$, meaning that $J$ was born before $I$. We consider again two cases.

    (2.1) Suppose $b <d$. This means that $J$ died after $I$. We also get $\mathrm{Hom}(\mathbf{k}^I, \mathbf{k}^J)\cong \mathbf{0}$. To prove this, we proced as before. Let $\alpha = (\alpha_t)_{t\in\mathbb{R}} \in \mathrm{Hom}(\mathbf{k}^I, \mathbf{k}^J)$. We know already that $\alpha_t = 0$ if $t\notin I\cap J$, so let $t\in I\cap J$. Then $\alpha_t$ is a linear map from $ \mathbf{k}$ to $\mathbf{k}$. By our assumptions, $I\cap J = I.$ Take the arrow $t\to d.$ By naturality of $\alpha$, we have

    \[\begin{align*} \alpha_t &= (\mathbf{k}\xrightarrow{\mathrm{Id}} \mathbf{k}) \circ \alpha_t\\ &= \mathbf{k}^J(t\to d)\circ \alpha_t \\ &= \alpha_d \circ \mathbf{k}^I(t\to d) \\ &= \alpha_d \circ (\mathbf{k}\xrightarrow{\mathrm{0}} \mathbf{0})\\ &= 0. \end{align*}\]

    Therefore $\alpha = \mathbf{0}$ and the assertion follows.

    (2.2) Suppose $d\leq b$. We can prove that $\mathrm{Hom}(\mathbf{k}^I, \mathbf{k}^J)\cong \mathbf{k}$. For each $\lambda\in \mathbf{k}$, define a morphism of persistence modules $\alpha^\lambda \colon \mathbf{k}^I\to \mathbf{k}^J$ by

    \[\alpha^\lambda_r = \begin{cases} \mathbf{k}\xrightarrow{\mu_\lambda}\mathbf{k} &\text{if } r\in I\cap J,\\ \mathbf{k}^I_r\xrightarrow{0}\mathbf{k}^J_r&\text{else} \end{cases}\]

    where $\mu_\lambda\colon r\mapsto \lambda r$. The map

    \[\Psi \colon \mathbf{k}\to \mathrm{Hom}(\mathbf{k}^I, \mathbf{k}^J):\lambda\mapsto \alpha^\lambda\]

    is injective, surjective, and linear.

Now we come to the following conclusion.

Fact 2. If $c\leq a\leq d\leq b$, then

\[\mathrm{Hom}(\mathbf{k}^{[a,b]}, \mathbf{k}^{[c,d]})\cong \mathbf{k}.\]

Both Fact 1 and Fact 2 will help us determine $d_T(\mathbf{k}^I, \mathbf{k}^J)$ for any closed intervals $I$ and $J$.

Upper bound

We start looking for values of $t\geq 0$ for which a $t$-interleaving of ${\mathcal{I}}=\mathbf{k}^I$ and ${\mathcal{J}}=\mathbf{k}^J$ exists, that is, for which we can find maps $\phi\colon {\mathcal{I}}\to {\mathcal{J}}[t]$ and $\psi\colon {\mathcal{J}}\to {\mathcal{I}}[t]$ that make the diagrams

tikzcd diagram

commute. By using the fact that a shift of an interval module is the interval module of the shifted interval (Example 4), we can redraw these diagram as

\begin{tikzcd}[column sep=1.25em] {\mathbf{k}^{[a,b]}} \arrow[rd, "\phi"'] \arrow[rr, "{\mathbf{k}^{[a,b]}[0\to 2t]}"] & & {\mathbf{k}^{[a-2t,b-2t]}} & \mathbf{k}^{[c,d]} \arrow[rd, "\psi"'] \arrow[rr, "{\mathbf{k}^{[c,d]}[0\to 2t]}"] & & {\mathbf{k}^{[c-2t,d-2t]}} \\ & {\mathbf{k}^{[c-t,d-t]}} \arrow[ru, "{\psi[t]}"'] & & & {\mathbf{k}^{[a-t,b-t]}} \arrow[ru, "{\phi[t]}"'] & \end{tikzcd}

The first observation is that if the top arrows are both $0,$, then we can choose $\phi=0$ and $\psi=0$ because then the triangles commute trivially. But, how do we get the top arrows to be zero? Here we can use Fact 1: if $[a,b]\cap [a-2t,b-2t]=\varnothing$, then

\[\mathrm{Hom}(\mathbf{k}^{[a,b]}, \mathbf{k}^{[a-2t,b-2t]}) = \mathbf{0}.\]

In order to get an empty intersection, we just need to make a sufficiently large shift. Since $t\geq 0$, the shift moves to the left, so we need $b-2t < a$, that is $t> \frac{b-a}{2}$.

By the same reason we arrive at $t> \frac{d-c}{2}$. Thus the top arrows are both zero if $t> \frac{b-a}{2}$ and $t> \frac{d-c}{2}$, which is equivalent to \(t>\frac{1}{2}\max\left\{ b-a,d-c \right\}.\) If we denote the right term by $M$, we get that an $(M+\varepsilon)$-interleaving of $\mathbf{k}^I$ and $\mathbf{k}^J$ exists for every $\varepsilon > 0$. Thus $d_T(\mathbf{k}^I, \mathbf{k}^J) \leq M+\varepsilon$ for every $\varepsilon > 0$, and taking the infimum over $\varepsilon$ give us

\[d_T(\mathbf{k}^{[a,b]}, \mathbf{k}^{[c,d]}) \leq \frac{1}{2}\max\left\{ b-a,d-c \right\}.\]

Notice that this bound does not take into account the position of the intervals respect to each other, so our next step is to find a bound that does consider this aspect.

Now we use Fact 2. Framed in our context, it tell us that

\[\begin{align*} c-t\leq a \leq d-t\leq b \;&\implies \mathrm{Hom}(\mathbf{k}^{[a,b]}, \mathbf{k}^{[c-t,d-t]})\cong \mathbf{k},\\ a-t\leq c \leq b-t\leq d \;&\implies \mathrm{Hom}(\mathbf{k}^{[c,d]}, \mathbf{k}^{[a-t,b-t]})\cong \mathbf{k} . \end{align*}\]

We start by looking for values of $t\geq0$ for which the two sets of inequalities are satisfied, because then we can choose appropriate nonzero $\phi$ and $\psi$ such that $(\phi,\psi)$ is a $t$-interleaving.

The conditions $c-t\leq a$ and $a-t\leq c$ are equivalent to $t\geq |c-a|$, and the conditions $d-t\leq b$ and $b-t\leq d$ are equivalent to $t\geq |d-b|.$ So, let $t\geq\max\left\{|c-a|,|d-b|\right\}$.

With regard to the middle inequalities, we consider two cases.

  1. Suppose $d-t < a$ and $b-t<c$. Using the fact that $t\geq |d-b|\geq b-d$, we get

    \[b-2t = b -t -t \leq b-(b-d)-t \leq d-t < a\]

    whence $t > \frac{b-a}{2}$. Similarly, from $b-t < c$ we get $t> \frac{d-c}{2}$. Thus

    \[t\geq \max\left\{\frac{b-a}{2},\frac{d-c}{2}\right\},\]

    which lead us to the situation above where a $t$-interleaving trivially exists, but the two hom-sets are zero.

  2. Suppose that $a\leq d-t$ or $c\leq b-t$. Since $t\geq\max\left\{|c-a|,|d-b|\right\}$, we see that either inequality implies the other. Thus we have $a\leq d-t$ and $c\leq b-t$. Therefore both sets of inequalities above are satisfied, whence

    \[\mathrm{Hom}(\mathbf{k}^{[a,b]}, \mathbf{k}^{[c-t,d-t]})\cong \mathbf{k} \cong \mathrm{Hom}(\mathbf{k}^{[c,d]}, \mathbf{k}^{[a-t,b-t]}).\]

    By Fact 2, this isomorphism implies that to $1\in \mathbf{k}$ there correspond persistence-module-morphisms $\phi\colon \mathbf{k}^{[a,b]}\to \mathbf{k}^{[c-t,d-t]}$ and $\psi\colon \mathbf{k}^{[c,d]}\to \mathbf{k}^{[a-t,b-t]}$ defined by

    \[\phi_r = \begin{cases} \mathbf{k}\xrightarrow{\mathrm{Id}}\mathbf{k} &\text{if } r\in [a,d-t],\\ \mathbf{0}&\text{else} \end{cases}\]

    and

    \[\psi_r = \begin{cases} \mathbf{k}\xrightarrow{\mathrm{Id}}\mathbf{k} &\text{if } r\in [c,b-t],\\ \mathbf{0}&\text{else} \end{cases}\]

    for each $r\in \mathbb{R}$.

    The final (and most important) step is to prove that $(\phi,\psi)$ is a $t$-interleaving of $\mathbf{k}^I$ and $\mathbf{k}^J$. This amounts to prove that the triangles

    \begin{tikzcd}[column sep=1em] {\mathbf{k}^{[a,b]}_r} \arrow[rd, "\phi_r"'] \arrow[rr, "{\mathbf{k}^{[a,b]}(r\to r+2t)}"] & & {\mathbf{k}^{[a-2t,b-2t]}_r} & {\mathbf{k}^{[c,d]}_r} \arrow[rd, "\psi_r"'] \arrow[rr, "{\mathbf{k}^{[c,d]}(r\to r+2t)}"] & & {\mathbf{k}^{[c-2t,d-2t]}_r} \\ & {\mathbf{k}^{[c-t,d-t]}_r} \arrow[ru, "{\psi_{r+t}}"'] & & & {\mathbf{k}^{[a-t,b-t]}_r} \arrow[ru, "{\phi_{r+t}}"'] & \end{tikzcd}

    commute for every $r\in \mathbb{R}$. Let’s consider the first triangle. We consider three cases.

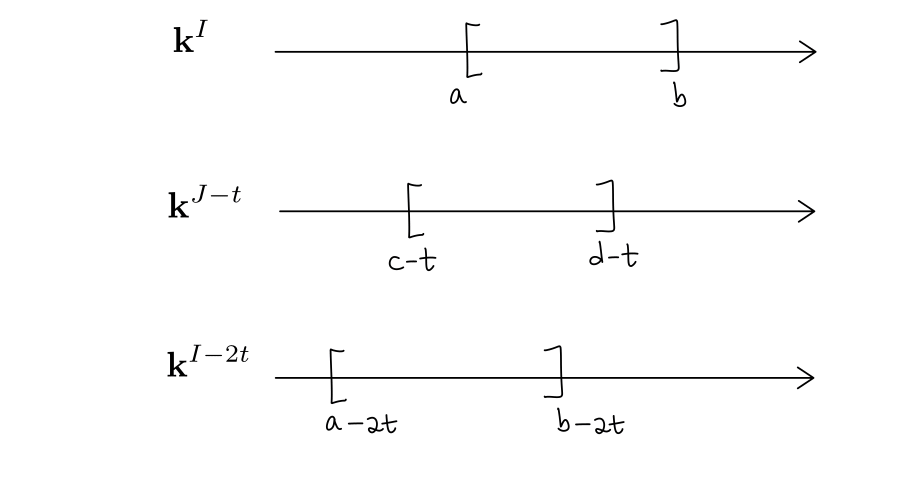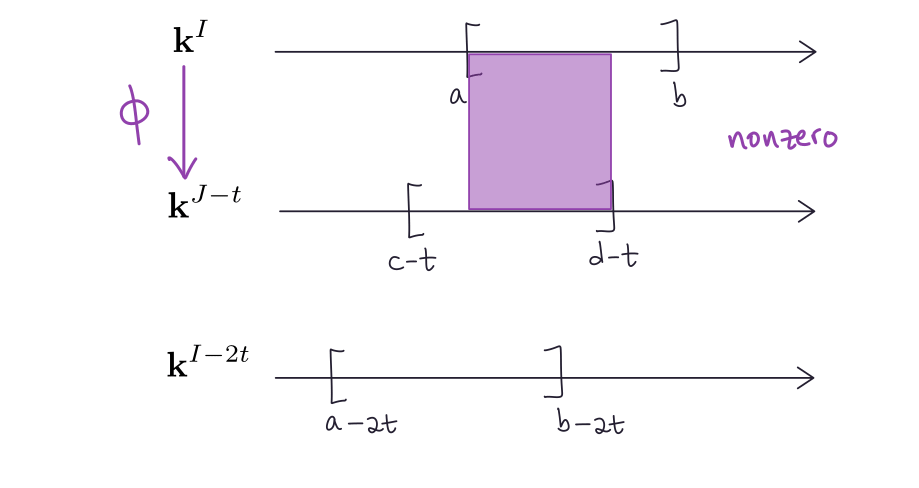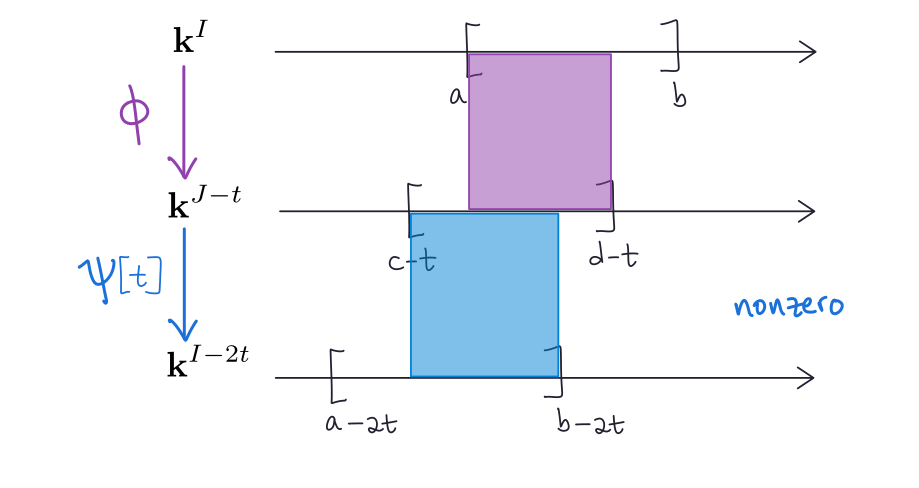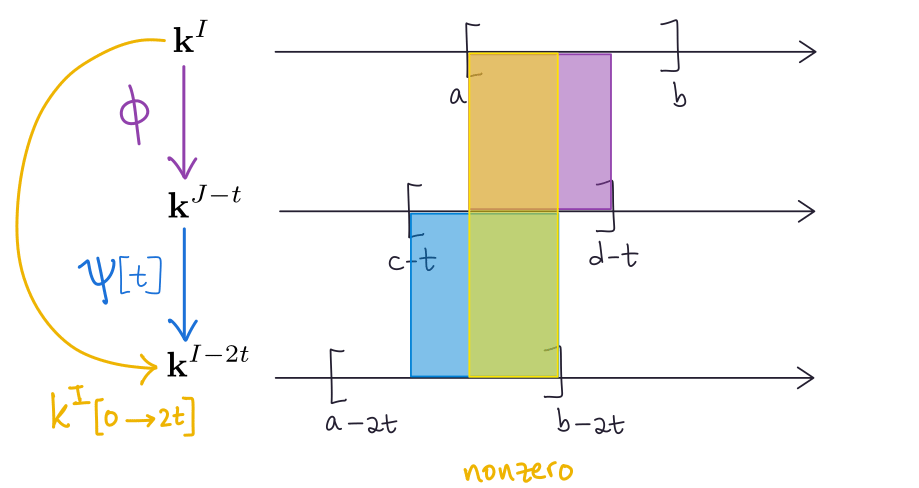
    diagram 7

    If $r\in (-\infty,a)$, then

    \[\begin{aligned} \psi_{r+t}\circ \phi_r &= \psi_{r+t}\circ (\mathbf{0}\xrightarrow{\mathrm{0}}\mathbf{k^*})\\ &= \mathbf{0}\xrightarrow{\mathrm{0}}\mathbf{k^*}\\ &= \mathbf{k}^{[a,b]}(r\to r+2t) \end{aligned}\]

    no matter the value of $\psi_{r+t}$. Here $\mathbf{k^*}$ denotes either $\mathbf{0}$ or $\mathbf{k}$.

    If $r\in[a,b-2t]$, then

    \[\begin{aligned} \psi_{r+t}\circ \phi_r &= (\mathbf{k}\xrightarrow{\mathrm{Id}}\mathbf{k}) \circ (\mathbf{k}\xrightarrow{\mathrm{Id}}\mathbf{k})\\ &= \mathbf{k}\xrightarrow{\mathrm{Id}}\mathbf{k}\\ &= \mathbf{k}^{[a,b]}(r\to r+2t). \end{aligned}\]

    Finally, if $r\in(b-2t,\infty)$,

    \[\begin{aligned} \psi_{r+t}\circ \phi_r &= (\mathbf{k^*}\xrightarrow{\mathrm{0}}\mathbf{0}) \circ \phi_r\\ &= \mathbf{k^*}\xrightarrow{\mathrm{0}}\mathbf{0}\\ &= \mathbf{k}^{[a,b]}(r\to r+2t). \end{aligned}\]

    where $\mathbf{k^*}$ denotes either $\mathbf{0}$ or $\mathbf{k}$. We have proved that the left triangle commutes for every $r\in \mathbb{R}$. In an entirely analogous manner we prove that the right triangle commutes. Therefore $(\phi,\psi)$ is a $t$-interleaving of $\mathbf{k}^{I}$ and $\mathbf{k}^J$.

We have proved that, in either case, $\mathbf{k}^{I}$ and $\mathbf{k}^J$ are $t$-interleaved if $t\geq\max\left\{|c-a|,|d-b|\right\}$. Thus

\[d_T(\mathbf{k}^{[a,b]}, \mathbf{k}^{[c,d]}) \leq \max\left\{ |c-a|,|d-b|\right\}.\]

Up to now we’ve found two upper bounds for $d_T(\mathbf{k}^{[a,b]}, \mathbf{k}^{[c,d]})$, so this distance is less than both bounds. We summarize what we’ve found in the following

Fact 3. For any closed intervals $I=[a,b]$ and $J=[c,d]$,

\[d_T(\mathbf{k}^{I}, \mathbf{k}^{J}) \leq \min\left\{ \frac{1}{2}\max\left\{ b-a,d-c \right\},\max\left\{ |c-a|,|d-b|\right\}\right\}.\]

Lower bound

Let’s prove that the last inequality is tight. Let

\[m = \min\left\{ \frac{1}{2}\max\left\{ b-a,d-c \right\},\max\left\{ |c-a|,|d-b|\right\}\right\}.\]

We want to show that if a $t$-interleaving exists, then necessarily $t\geq m$, for then we can take the infimum over all those $t\geq 0$ and get that $d_T(\mathbf{k}^{[a,b]}, \mathbf{k}^{[c,d]})\geq m$.

Suppose that $(\phi, \varphi)$ is a $t$-interleaving of $\mathbf{k}^{[a,b]}$ and $\mathbf{k}^{[c,d]}$.

Either

\[t \geq \frac{1}{2}\max\left\{ b-a,d-c \right\}\]

or

\[t < \frac{1}{2}\max\left\{ b-a,d-c \right\}.\]

In the first case we get $t\geq m$ immediatly because of the definition of $m$, a minimum.

Let us focus on the second case. Suppose that $t < \frac{1}{2}\max\left\{ b-a,d-c \right\}.$ Let us assume, without loss of generality, that $b-a \geq d-c $. We know that the diagram

\begin{tikzcd}[column sep=1em] {\mathbf{k}^{[a,b]}_r} \arrow[rd, "\phi_r"'] \arrow[rr, "{\mathbf{k}^{[a,b]}(r\to r+2t)}"] & & {\mathbf{k}^{[a-2t,b-2t]}_r} \\ & {\mathbf{k}^{[c-t,d-t]}_r} \arrow[ru, "\psi_{r+t}"'] & \end{tikzcd}

commutes for every $r\in \mathbb{R}$. Moreover, the top arrow is nonzero when $r\in [a,b]$ and $r\in [a-2t,b-2t]$, i.e., when

\[r\in [a,b] \cap [a-2t,b-2t] = [a,b-2t].\]

Notice that $[a,b-2t]\neq \varnothing$ because $t < \frac{b-a}{2}$ by assumption. Let $r\in [a,b-2t]$. Our last diagram becomes

\begin{tikzcd}[column sep=1em] \mathbf{k} \arrow[rd, "\phi_r"'] \arrow[rr, "\mathrm{Id}"] & & \mathbf{k} \\ & {\mathbf{k}^{[c-t,d-t]}_r} \arrow[ru, "\psi_{r+t}"'] & \end{tikzcd}

whence $\psi_{r+t}\circ \phi_r = \mathrm{Id}$. Since $\mathrm{Id}$ is injective, so is $\phi_r$. Since $\mathrm{Id}$ is surjective, so is $\psi_{r+t}$. Either of these facts imply that $\mathbf{k}^{[c-t,d-t]}_r$ is not zero, and thus $\mathbf{k}^{[c-t,d-t]}_r = \mathbf{k}$, necessarily. By definition of interval module, we get

\[\mathbf{k}^{[c-t,d-t]}_r = \mathbf{k} \iff r\in [c-t,d-t].\]

Therefore $r\in [c-t,d-t]$. We have shown that $[a,b-2t]\subset [c-t,d-t]$, which translated into inequalities give us

\[\begin{equation}\label{eq1} t > c-a \quad\text{and}\quad t > b-d. \end{equation}\]

Furthermore, since $b-a\geq d-c$, we have

\[c-a \geq d-b \quad\text{and}\quad b-d \geq a-c.\]

It follows that

\[\begin{equation}\label{eq2} t > d-b \quad\text{and}\quad t > a-c. \end{equation}\]

Combining \eqref{eq1} and \eqref{eq2}, we get

\[t \geq |c-a| \quad\text{and}\quad t \geq |d-b|\]

which is equivalent to

\[t \geq \max\{|c-a|, |d-b|\}.\]

Therefore $t\geq m$, as we wanted show.

We obtain our desired conclusion:

For any closed intervals $I=[a,b]$ and $J=[c,d]$,

\[d_T(\mathbf{k}^{I}, \mathbf{k}^{J}) = \min\left\{ \frac{1}{2}\max\left\{ b-a,d-c \right\},\max\left\{ |c-a|,|d-b|\right\}\right\}.\]